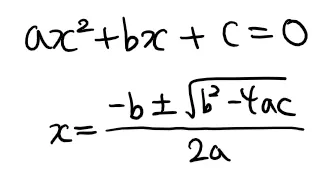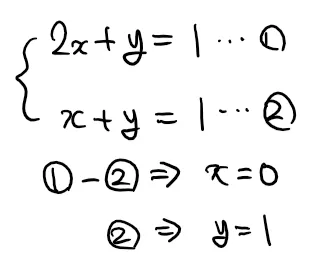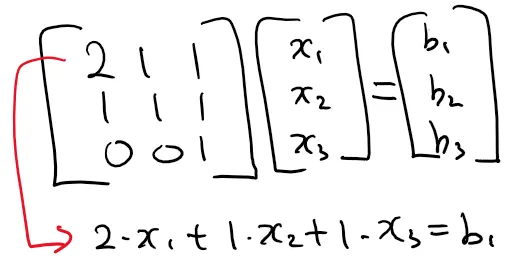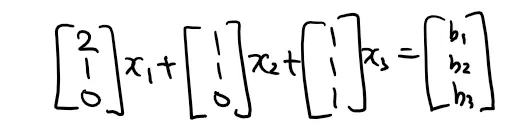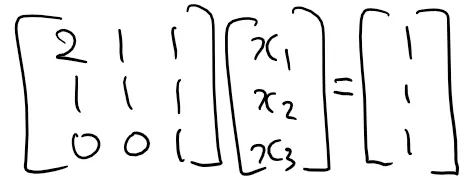History
2020.05.23 | 초안 작성 |
개요
많은 사람들의 선형대수 스승일 Gilbert Strang은 학부 시절 계산만 해서 몰랐던 혹은 까먹었을 선형대수의 많은 부분들을 알려주고 계시다. 이 글에서 다뤄보고 싶은 내용은 Strang이 Unit 1: AX=B AND The Four Subspces에서 특히 강조하는 Column Space Picture에 대한 것이다.
선형대수 시리즈로 적어보면 좋겠는데 과연... 내가 그렇게 부지런할지는...
허수(Imaginary Value)란 무엇인가?
선형대수에서 뜬금없이 허수를 언급해서 이상하다고 생각할 사람이 많을 것 같다. 하지만 내가 수업을 들으며 Column Space Picture를 이해한 바가 허수의 의미에 대해 예전에 읽었던 내용과 관련이 있다. 그래서 우선 허수가 무엇이고 왜 필요한지에 대해서 이야기 해보고자 한다.
근의 공식
우리가 중등수학에서 처음으로 허수와 가까워질 때는 이차방정식의 일반해를 위해 근의 공식을 배울 때이다.
요즘 교육과정이 어떤지는 모르겠지만 나는 중등수학에서는 판별식 b^2 - 4ac가 양수이면 두 개의 근, 0이면 1개의 중근, 음수이면 해가 존재하지 않는다고 배웠다.
그리고 고등수학에 와서야 허수를 배우며 '사실 이차방정식에는 항상 2개의 해가 존재합니다 짜잔!'이라고 배웠던 기억이 난다.
그리고 이는 고차방정식으로 확장되어 n차 방정식(n-th order equation)은 n개의 해를 가진다는 결론에 다다를 수 있게된다. 즉, 우리는 허수의 존재를 통해 좀더 완전한 결론에 다가갈 수 있게 된 것이다.
분수와 소수(Decimal)는 실재하는가?
근의 공식은 내가 이해하고 있는 바를 완전히 설명하는 예시는 아니어서 결국 위의 글에서 이야기하는 또 다른 예시를 가져와서 설명해보고자 한다.
분수(fraction)혹은 소수(Decimal) 대해서 생각해본다면 이건 실재하는 수라고 할 수 있을까? 사과 3/5개, 여자친구 1.2명, 이런 것들은 존재할 수 없다.
어떤 사람이 하프 샌드위치(half sandwich)를 주문한다고 생각해보자. 어떻게 절반의 샌드위치를 시킬 수 있나? 다른 손님의 샌드위치를 절반 빼앗아오나? 아니면 다른 손님이 하프 샌드위치를 하나 더 주문할 때까지 기다렸다가 받을 수 있는걸까?(feat. The Big Bang Theory - Sheldon & Penny Funny Half Sandwich - YouTube) 사실 우리는 분수나 소수를 말할 때 내가 상상하는 전체에 대한 특정 비율(ratio)을 의미하고 있음을 알 수 있다.
수학적 도구로의 분수와 소수
현대물리학에 의하면 불연속적인 이 세상에서는 분수나 소수는 실재하지 않는다. 하지만 세상을 분석하는데 굉장히 유용한 도구가 된다. 위의 글에서는 다음과 같은 예시를 이야기한다.
•
인구집단 A는 236명이며 그 중 48명이 어린이다.
•
인구집단 B는 1234명이며 그 중 123명이 어린이다.
•
인구집단 A의 어린이의 값(the fraction of children in population A)는 48/236이며 인구집단 B의 어린이의 값은 123/1234이다.
•
48/236(대략 0.2)는 123/1234(대략 0.1)보다 훨씬 크다
•
인구집단 A는 인구집단 B보다 0.1만큼 더 젊다고 할 수 있다.
이 때 인구집단 C,D,E가 존재한다고 하면 우리는 집단 내 어린이 비율을 통해 어떤 집단이 다른 집단보다 얼마나 더 젊은지 등을 분수를 통해 비교할 수 있다.
이와 마찬가지로 허수 또한 실재하지 않는 수지만 우리가 세상을 더 잘 이해할 수 있는 수학적 도구가 되어준다.
수의 그림자를 들여다 봄으로써 우리는 수면 위의 수들이 어떻게 움직이는지 더 깊게 이해할 수 있습니다.
The Column View of the linear algebra
AX = B를 이해하는 첫번째 방법, Row View
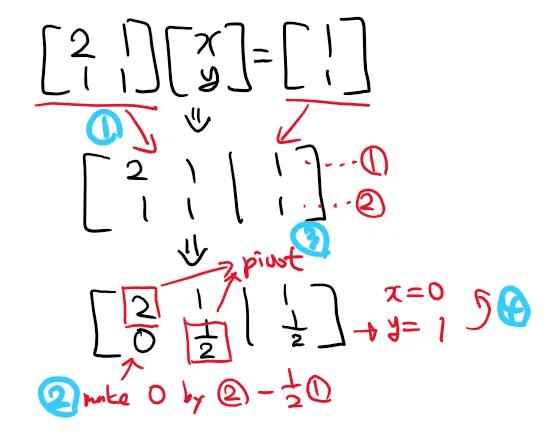
우리는 중등수학에서 일차연립방정식을 가우스 소거법으로 푼다. 다시말해, 미지수를 제거하고 구한 미지수의 값을 하나씩 대입해서 연립 방정식을 해결하게 된다.
이 강의를 듣는 랩메이트 중 한명이 어릴 때 미국에서 살다와서 종종 미국의 수학 교육과정 이야기를 듣게되는데 미국에서는 연립방정식을 배울 때 Elimination을 함께 배운다. 우리가 미지수를 이용해서 하는 가우스 소거법을 행렬을 이용해서 한다.
•
파란색 1: 연립방정식을 행렬화 한뒤
•
파란색 2: 행렬의 왼쪽 아래 부분을 모두 0으로 만든다.(nxn에서는 왼쪽 아래가 여러 개가 될 수 있다.)
•
파란색 3: 대각선의 아이들은 pivot이 된다.
•
파란색 4: 아래쪽에서 차례로 올라가며 대입해서 각 미지수를 구한다.
이와 같이 AX = B는 일차 연립방정식을 가우스 소거법으로 풀기위한 도구로 이해될 수 있다.
AX = B를 이해하는 두번째 방법
첫번째 방법에서는 행렬(Matrix)의 각 행(Row)이 어떤 연립 일차 방정식 미지수와 곱해진다고 본다. 즉 각 행의 원소(element)들이 해당 미지수들의 계수(coefficient)로 이해될 수 있다. 그래서 AX = B를 이해하는 Row View가 된다.
이 내용은 너무나 익숙하기 때문에 Gilbert Strang은 Unit 1에서 상대적으로 Column View를 많이 강조하신다.
Row View에서는 각 행을 미지수의 계수로 가지는 연립방정식이었던 반면, Column View에서는 각 행을 벡터(vector)로 생각할 때 이들의 선형 결합(linear combination)으로 생각할 수 있다. 이제 우리는 AX = B를 다음과 같이 시각화 할 수 있다.
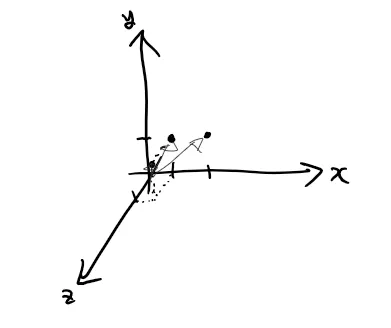
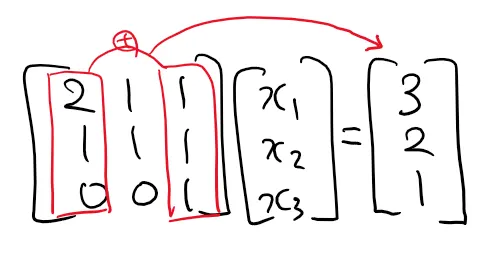
그럼 우리는 이제 Column View를 이용해서 아래와 같은 B에 대해서는 쉽게 답할 수 있다. 세번째 열의 vector와 B가 똑같기 때문에 X = [0, 0, 1]이 답이 된다.
혹은 이런 것도! 첫번째 열의 vector와 세번째 열의 vector를 더하면(선형결합) B가 되기때문에 X = [1, 0, 1]이 답이 된다.
즉 AX = B는 A의 Column Vector들을 어떻게(X) 선형 결합을 시켜야 B가 되는가를 찾는 문제로 해석할 수도 있다.
결론
마치 우리가 분수나 허수를 통해 실제 세상의 더 잘 이해할 수 있듯이, Column View도 행렬을 이해할 수 있는 수학적 도구로써 작동한다.
사실 Column View라는 거 자체는 굉장히 별 거 없어서 다른 예시들도 넣고 싶었는데... 그러니까 글이 너무 길어져서 미루기로 했다.
다음 글에서는 Column View를 기반으로 Column Space와 가능하다면 Four Spaces에 대해서 얘기해볼 예정이다. 그 다음에는 AX = B의 해가 어떻게 존재하는지(e.g. 없음, 하나임, 무한히 많음)를 고려하는 전체 그림에 대해서도!